Electrical Engineering
　
Welcome Biography Research Teaching Publications Awards
Lab Professional Activities Research Projects Links

Graph Drawing and Computational Geometry 

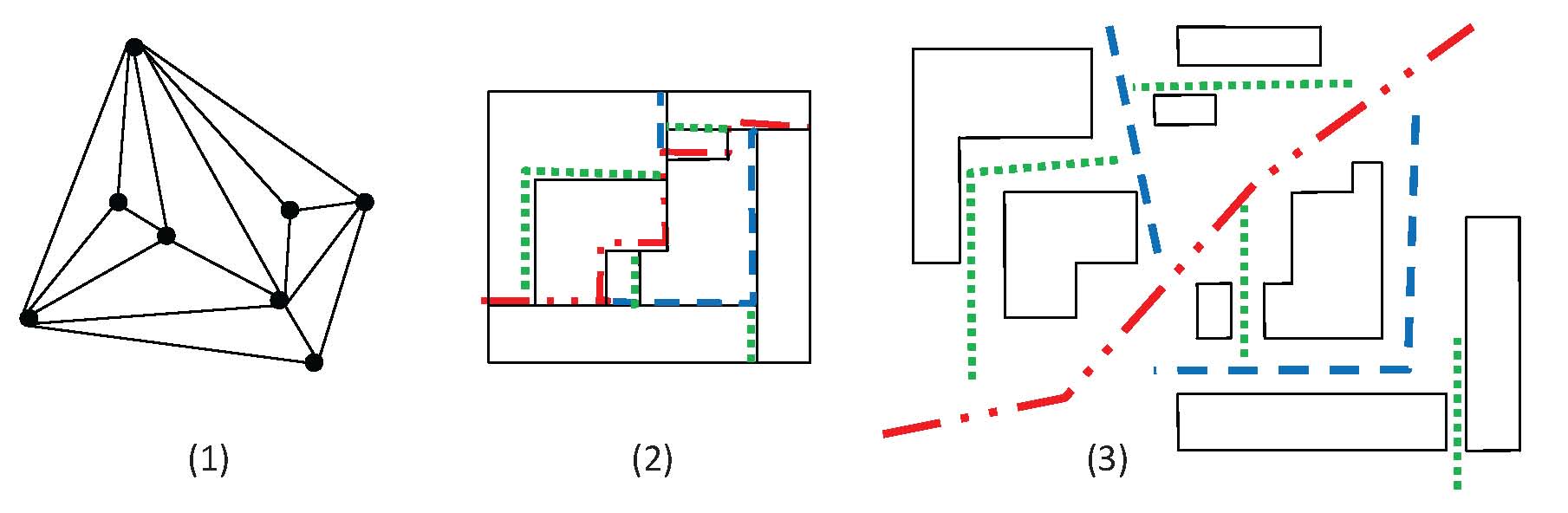
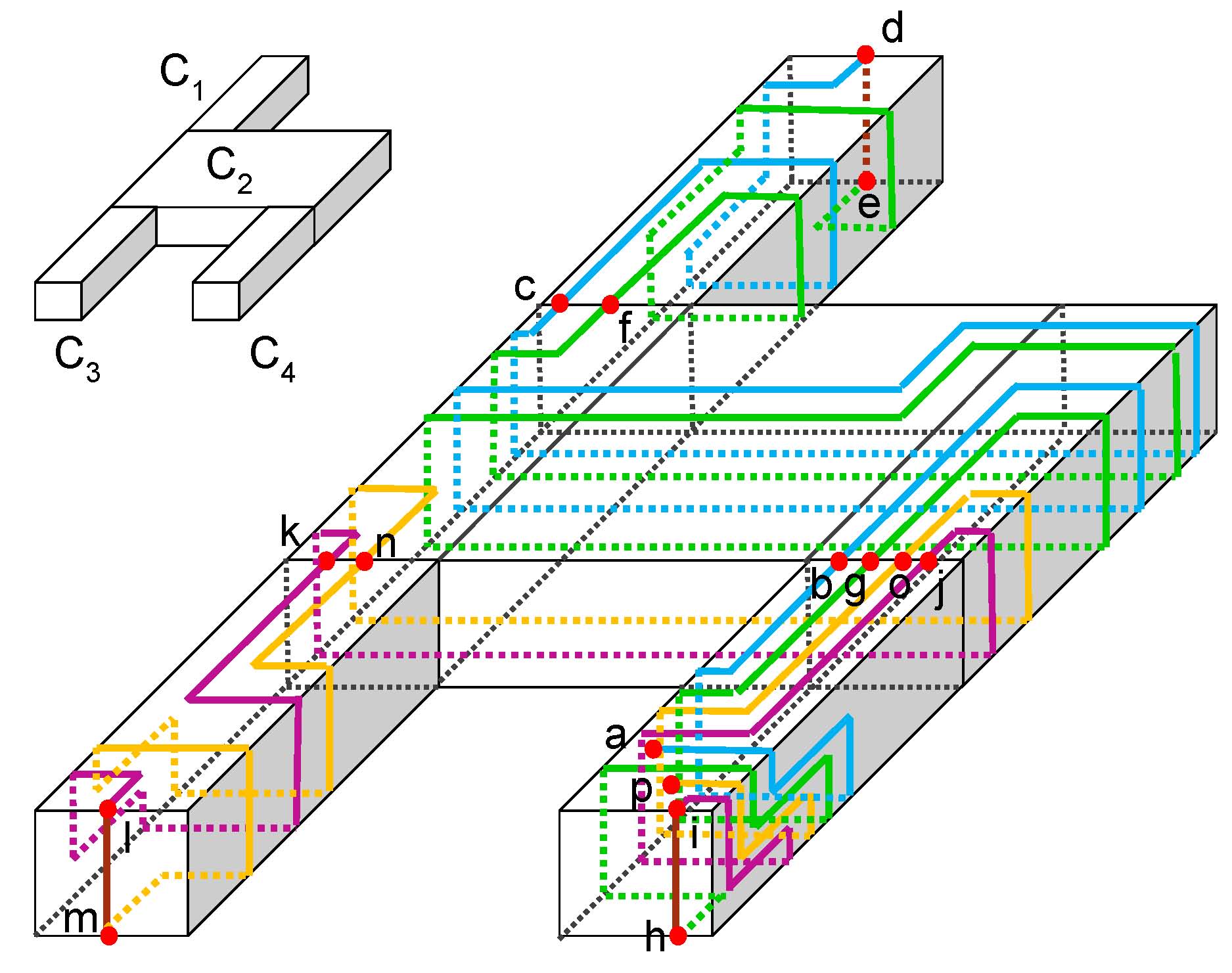
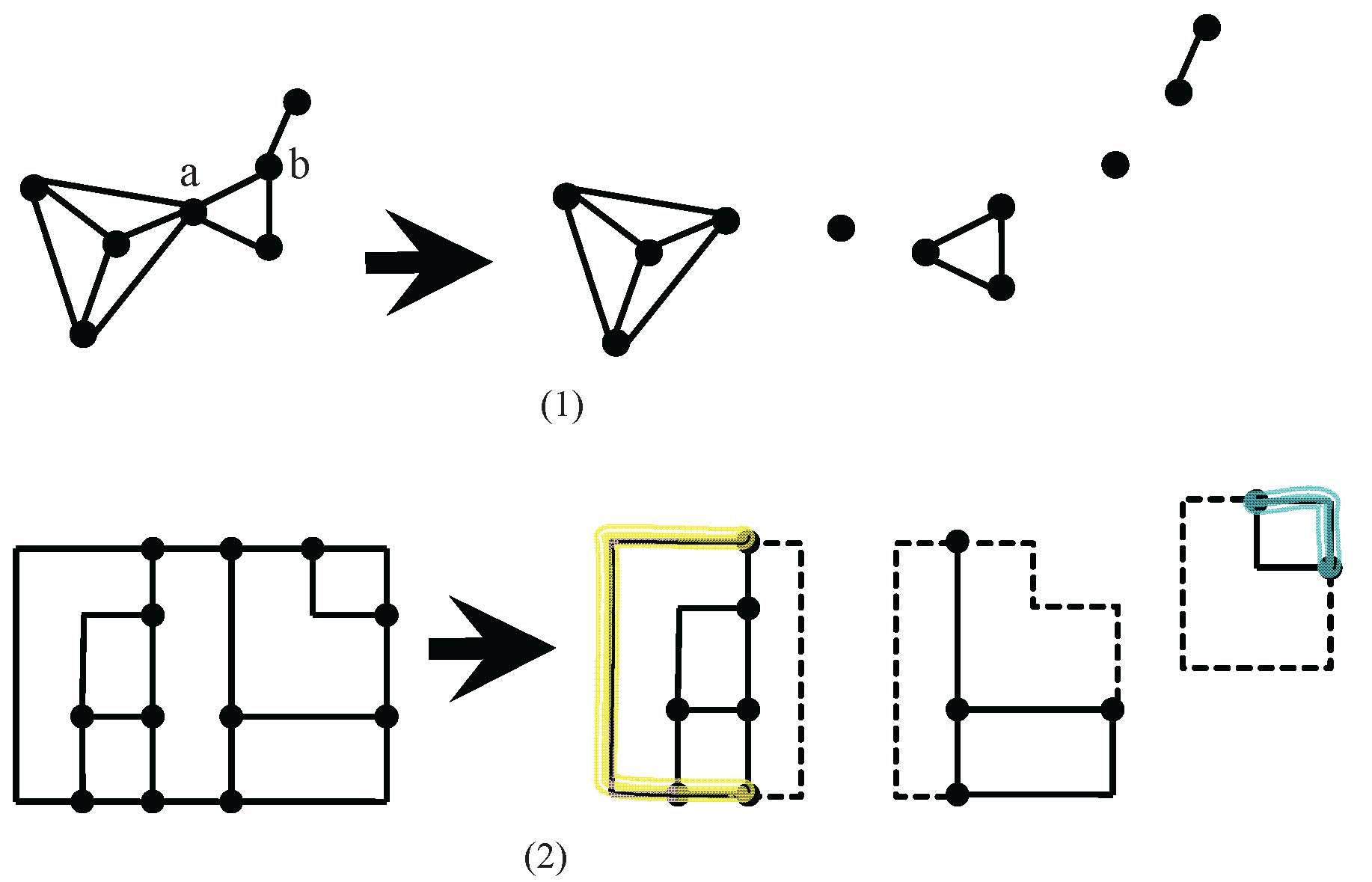
Graphs represent one of the most popular abstract models in describing complex science and engineering problems. Graph drawing refers to the process of displaying an abstract graph in 2D or 3D, allowing the structure as well as the meaning of the graph to be understood better and easier. As a consequence, the design of graph drawing algorithms has become an emerging and fast growing research area in computer science. Our research focuses on algorithmic aspects of graph drawing, including

  • Contact Representations of Planar Graphs
  • Design and Analysis of Graph Drawing Algorithms
  • Floorplan Design in 2D and 3D
  • Unfolding Polyhedra

Selected publications

Y. Chang, and H. Yen, Constrained floorplans in 2D and 3D, Theoretical Computer Science, Vol. 607, Part 3,  320-336, 2015.

Y. Chang, and H. Yen, A New Approach for Contact Graph Representations and Its Applications, 14th Int'l Symp. on Algorithms and Data Structures (WADS 2015), Victoria, Canada, Aug. 2015.

Y. Chang, and H. Yen, Improved Algorithms for Grid-unfolding Orthogonal Polyhedra,  International Journal of Computational Geometry & Applications, Vo. 27, No 1 & 2, 33-56,  2017

Y. Chang, and H. Yen, On Orthogonally Convex Drawings of Plane Graphs, COMPUTATIONAL GEOMETRY: Theory and Applications, Vol. 62,  34–51, April 2017.

S. Takahashi, H. Wu, S. Saw, C. Lin,  and H. Yen, Optimized Topological Surgery for Unfolding 3D Meshes. Comput. Graph. Forum 30 (7): 2077-2086, 2011.

　

Information Visualization 

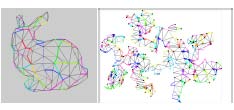
The aim of Information visualization focuses on the study of visual representations of abstract data in order to help people in exploring, analyzing, and understanding the data. We are interested in both theoretical foundations as well as practical applications of  information visualization.

  • Metro Map Layout and Annotation
  • Boundary Labeling
  • Force-directed Drawing Algorithm
  • Mental-Map Preserving Visualization Technique

Selected publications

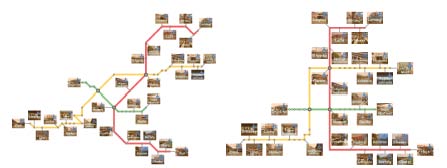
H. Wu, S. Takahashi, D. Hirono, M. Arikawa, C. Lin, and H. Yen, Spatially Efficient Design of Annotated Metro Maps, Computer Graphics Forum,   Vol. 32, No. 3, pp. 261-270, 2013.

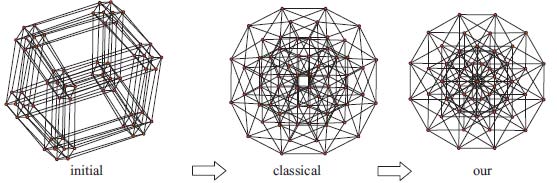
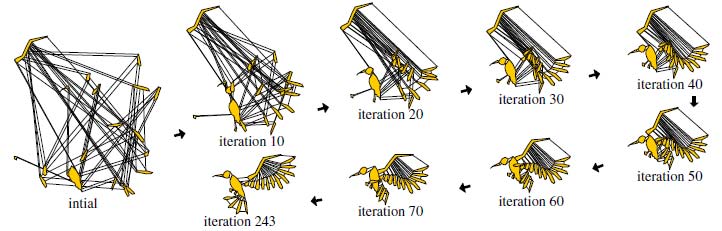
C. Lin and H. Yen, A New Force-Directed Graph Drawing Method Based on Edge-Edge Repulsion,  Journal of Visual Languages and Computing, Vol. 29, No. 1, pp. 29-42, 2012.

C. Lin, Y. Lee, and H. Yen, Mental Map Preserving Graph Drawing Using Simulated Annealing, Information Sciences, Vol. 181, No. 19, pp. 4253-4272, 2011.

C. Lin, H. Yen, and J. Chuang, Drawing Graphs with Nonuniform Nodes Using Potential Fields, Journal of Visual Languages and Computing, Vol. 20, No. 6, 385-402, 2009.

C. Lin, H. Kao, and H. Yen, Many-to-One Boundary Labeling,   Journal of Graph Algorithms and Applications, Vol. 13, No. 3,  319-356, 2008.

　

Additional Research Interests

 Automata Theory and Formal Languages

Among various mathematical models that have been proposed in the disciplines of computer science and engineering, automata represent the most popular abstract model whose study dated back to the early 60s and since then, a rich body of deep and exciting results have been accumulated in the literature with respect to a wide variety of automata and their respective languages. In the past decade, the mainstream in the research on automata theory and formal languages has gradually switched from pure theoretical studies (such as issues related to expressive power, language hierarchies, closure properties and decision problems, etc) to a more balanced research between theory and application, in particular, applying various automata (and the theory behind them) to reasoning about the behaviors and computations of real-world hardware/ software systems.

Membrane Computing

Membrane computing (MC) identifies an unconventional  computing model from natural phenomena of cell evolutions and chemical reactions. MC has a great potential for implementing massively  parallel systems in an efficient way that would allow us to solve currently intractable problems once future bio-technology (or silicon-technology) gives way to a practical bio-realization (or  chip-realization). In our study,  we investigate various computational issues related to  MC, establishing the following results:

  • •nonuniversality of deterministic catalytic systems
  • •model-checking of signaling membrane systems
  • •identifying computational power of membrane systems w.r.t. various notions of parallelism...

 Petri Net Theory

Petri nets, introduced by C. A Petri in 1962, provide an elegant and useful mathematical formalism for modelling concurrent systems and their behaviors. In many applications, however, modelling by itself is of limited practical use if one cannot analyze the modelled system. As a means of gaining a better understanding of the Petri net model, the decidability and computational complexity of typical automata theoretic problems concerning Petri nets have been extensively investigated in the literature in the past four decades. Our research on Petri nets focuses on decidability/complexity analysis of various problems associated with Petri nets (equivalently,  vector addition systems, vector replacement systems, and vector addition systems with states).